Strikes Tournament Simulation Results

[gammagoat]

When did this change? News to me

Question on IFPA Tournament Finals Formats

That is really the rule. 3 strikes events especially can vastly vary round to round with how many 4 player groups are actually formed. It would be too difficult and time consuming to calculate that average every single round. If the tournament is designed to be 4 player groups wherever possible it gets the benefit of the doubt on the 2x multiplier.

[pinwizj]

Keefer’s simulator changed how we handled it. Strikes tournaments were overvalued the old way.

[raydaypinball]

What about the 17 player x number rounds of match play, I assume that is only 1.5x multiplier? Even though match play tried to do groups of four?

[pinwizj]

@raydaypinball

What about the 17 player x number rounds of match play, I assume that is only 1.5x multiplier? Even though match play tried to do groups of four?

[LOTR_breath]

Match Play Qualifying

• 1 game added to TGP per game played for Head-to-Head matches
• 1.5 games added to TGP per game played for 3-player style matches (if a majority of groups are 3-player groups)
• 2 games added to TGP per game played for 4-player style matches (if a majority of groups are 4-player groups)
• If there are an equal number of 2-player and 3-player matches there is no multiplier
• If there are an equal number of 3-player and 4-player matches there is a 1.5X multiplier
• Please note this format does not require a finals component as the qualifying portion already consists of DIRECT play. This is often found in Swiss style formats where there is no separate distinct finals component.
• Please note the qualifying portion of the tournament can be added to the TGP calculation only if that qualifying portion reduces the field of participants by 50% or more

[FuzzyChord]

In case anyone’s interested in seeing the Mathematica code I used, here it is (including the narrower game score distribution to better separate skill levels, as well as sudden death for progressive strikes).

(* create a new player with a random skill level, 0 strikes/games *)
(* {playerID, skill, {round opponents}, strikes} *)
MakePlayer[ID_] := {ID, RandomVariate[LogNormalDistribution[0, 0.25]], {}, 0}

(* create a list of n new players *)
MakePlayers[n_] := MakePlayer[#] & /@ Range[n]

(* game score for a single player *)
GameScore[skill_] := RandomVariate[LogNormalDistribution[skill, 0.25]]

(* game scores for all players *)
GameScores[players_] := GameScore[#[[2]]] & /@ players

(* rank players by game score *)
GameRanking[players_] := Module[{scores, sortedScores, ranks},
  scores = GameScores[players];
  sortedScores = Reverse@Sort@scores;
  ranks = Flatten[FirstPosition[sortedScores, #] & /@ scores];
  Return@ranks
]

(* run game for multiple players, update records & strikes *)
RunGame[players_, suddenDeath_] := 
 Module[{playerIDs, skills, roundResults, strikes, ranks, updatedStrikes, newRoundResults, updatedRoundResults, updatedPlayers},
  {playerIDs, skills, roundResults, strikes} = Transpose@players;
  ranks = GameRanking[players];
  newRoundResults = DeleteCases[playerIDs, #] & /@ playerIDs;(* list of opponents for each player *)
  updatedRoundResults = MapThread[Append[#1, #2] &, {roundResults, newRoundResults}];
  updatedStrikes = strikes + Switch[
     1,
     1, If[suddenDeath, 2 (ranks - 1), ranks - 1],(* 1 strike for each loss, doubled if sudden death *)
     2, Switch[#, 1, 0, Length@players, 2, _, 1] & /@ ranks,(* fair strikes: 1st gets 0, last gets 2, else 1 *)
     3, Sign[ranks - 1](* everyone except 1st gets a strike *)
     ];
  updatedPlayers = Transpose@{playerIDs, skills, updatedRoundResults, updatedStrikes};
  Return@updatedPlayers
]

(* partition players into groups of up to n, avoiding singletons *)
PartitionPlayers[players_, n_] := Module[{nPlayers, remainingPlayers, groups, finalPartition},
  nPlayers = Length@players;
  remainingPlayers = players;
  groups = {};
  If[nPlayers <= n,(* if players fit on one game *)
   AppendTo[groups, remainingPlayers];
   remainingPlayers = {};
 ];
  While[Length@remainingPlayers > LCM[n, n - 1],(* while excess players exist *)
   AppendTo[groups, Take[remainingPlayers, n]];(* take n of them *)
   remainingPlayers = Drop[remainingPlayers, n]
 ];
  finalPartition = First@SortBy[Select[IntegerPartitions[Length@remainingPlayers], Max@# <= 4 &], Length@# - Min@# &];(* partition final players to maximize minimum group size *)
  Do[
   AppendTo[groups, Take[remainingPlayers, finalPartition[[i]]]];(* take up to n of them *)
   remainingPlayers = Drop[remainingPlayers, finalPartition[[i]]], {i, 1, Length@finalPartition}
 ];
  Return@groups
]

(* run tournament round with nPerGame players per game *)
RunRound[players_, nPerGame_, suddenDeath_] := 
 Module[{groups, updatedGroups},
  groups = PartitionPlayers[players, nPerGame];
  updatedGroups = RunGame[#, suddenDeath] & /@ groups;
  Return@Flatten[updatedGroups, 1]
]

(* shuffle players and sort by strikes *)
SortByStrikes[players_] := SortBy[RandomSample[players], Last]

(* run tournament with nStrikes to be ejected *)
RunTournament[players_, nPerGame_, nStrikes_] := 
 Module[{nRounds, remainingPlayers, removedPlayers, suddenDeath},
  nRounds = 0;
  remainingPlayers = players;
  removedPlayers = {};
  suddenDeath = False;(* flag set when 2 players remain *)
  While[Length@remainingPlayers > 1,
   nRounds++;
   If[Length@remainingPlayers < 3, suddenDeath = True];(* 2 players left \[Rule] sudden death *)
   remainingPlayers = RunRound[remainingPlayers, nPerGame, suddenDeath];
   removedPlayers = Join[removedPlayers, Reverse@Select[remainingPlayers, Last@# >= nStrikes &]];
   remainingPlayers = Select[remainingPlayers, Last@# < nStrikes &];
   remainingPlayers = SortByStrikes[remainingPlayers]
 ];
  Return@{nRounds, remainingPlayers, removedPlayers}
]

(* run Monte Carlo simulation of many tournaments to find duration (in rounds) *)
RunMonteCarloRounds[nPlayers_, nPerGame_, nStrikes_, nSims_] := 
 Module[{results},
  results = ParallelTable[First@RunTournament[MakePlayers[nPlayers], nPerGame, nStrikes], {i, 1, nSims}];
  Return[results]
]

(* run tournament and calculate Kendall Tau coefficient of final rankings *)
TournamentKendall[nPlayers_, nPerGame_, nStrikes_] := 
 Module[{nRounds, remainingPlayers, removedPlayers, IDs, skills, roundResults, strikes},
  {nRounds, remainingPlayers, removedPlayers} = RunTournament[MakePlayers[nPlayers], nPerGame, nStrikes];
  {IDs, skills, roundResults, strikes} = Transpose@Join[removedPlayers, remainingPlayers];
  Return@KendallTau[Range[nPlayers], skills]
]

Once these functions are loaded, simulations can be run like this:

(* generate statistics on a specific tournament config *)
nPlayers = 33;
nPlayersPerGame = 4;
nStrikes = 10;
nSims = 5000;
data = RunMonteCarloRounds[nPlayers, nPlayersPerGame, nStrikes, nSims];
mean = N@Mean@data
stdev = N@Sqrt@Variance@data;
cov = stdev/mean;
SortBy[Tally[data], First] // TableForm // Print
hist = Histogram[data, Automatic, "ProbabilityDensity"];
dist = EstimatedDistribution[data, JohnsonDistribution["SB", \[Gamma], \[Delta], \[Mu], \[Sigma]]]
Show[hist, Plot[PDF[dist, x], {x, 0, 30}, PlotRange -> All]]

[FuzzyChord]

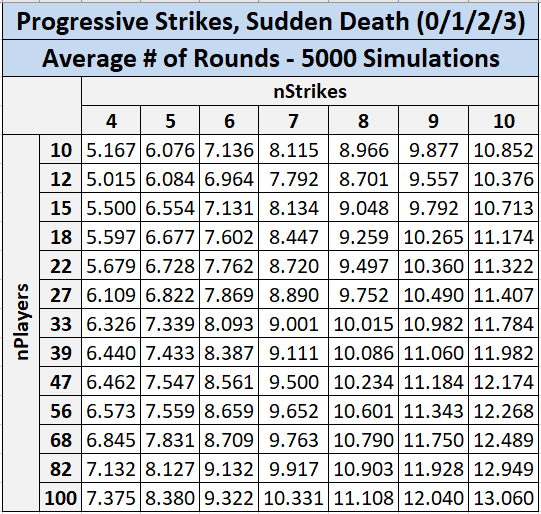
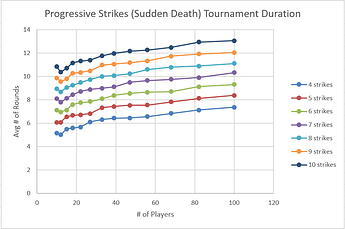
Since I added ‘sudden death’ rules to the Progressive Strikes code (doubling the assigned strikes when only 2 players remain), I recalculated the average round lengths:

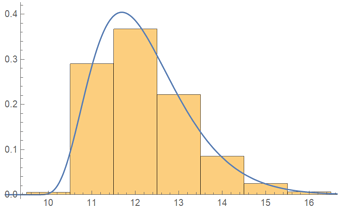
I also re-did the variance calculation. Here is the distribution of round numbers for the 47-player 10-progressive-strikes tournament:

Average duration = ~12.1888 rounds

• 10 rounds: 25 sims
• 11 rounds: 1451 sims
• 12 rounds: 1836 sims
• 13 rounds: 1111 sims
• 14 rounds: 426 sims
• 15 rounds: 122 sims
• 16 rounds: 29 sims

Relative to Progressive Strikes without sudden death, the average duration decreased by only ~0.4 rounds, but the far end of the right tail now terminates at 16 rounds, instead of 21. Quite a large drop!

[umbilico]

@gammagoat

It is interesting how different your results are to TGP Guide

@FuzzyChord

They may be measuring something different than I am to determine TGP value.

The results aren’t actually that different—I cross checked some of your values with the simulator the TGP guide is based on, and you’re getting pretty much the same numbers for rounds played. The TGP guide doesn’t list rounds played, though, only games towards TGP, which includes the time multiplier, but you can get the sim’s average rounds played from https://strikestgp.slapsave.com/.

@FuzzyChord

Do you know how the simulation chooses to count a round at 1X, 1.5X, or 2X?

While, as others have mentioned, the official rules say that the whole round gets counted as 1 / 1.5 / 2 games towards TGP, depending on whether the round’s games are a majority 2P / 3P / 4P games, the TGP guide’s simulator doesn’t actually look at that majority, but at each individual game.

I.e. it counts each individual 4P game as 2 games towards TGP, each 3P game as 1.5 games towards TGP, and so on, then calculates the average games towards TGP across all the games of all the rounds of all the simulator runs. That then is what the average number of total rounds played across all sim runs gets multiplied with in order to determine total games towards TGP for the format. Probably not that big of a difference to the majority thing, but might be interesting to look into.

[FuzzyChord]

This gives me a lot of confidence that my simulation was coded correctly. And it’s very interesting news that the TPG value of each game in a round is averaged together to determine the round’s TGP contribution. Is that how the official TPG table is generated?

I will try to add a TPG calculation to my simulation.

[umbilico]

@FuzzyChord

And it’s very interesting news that the TPG value of each game in a round is averaged together to determine the round’s TGP contribution. Is that how the official TPG table is generated?

Yes, but you gotta be careful, the way you worded it is not quite correct: The simulator doesn’t ever determine any particular round’s TGP contribution, it averages across all games of all rounds of all sim runs. This probably makes a real difference for the results, because the late rounds will have a high relative but low absolute number of less-than-4P-games.

Simple example, 32 players play Oprah strikes for 1 strike total, i.e. 1st round has 32 players, 2nd has 8, 3rd has 2. By determining each round’s games towards TGP separately, you’ll get 5 exactly, but the simulator will get you 5.73, which the TGP guide will round to 6.