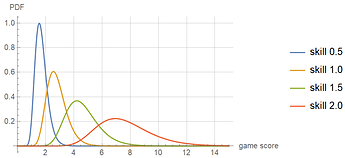
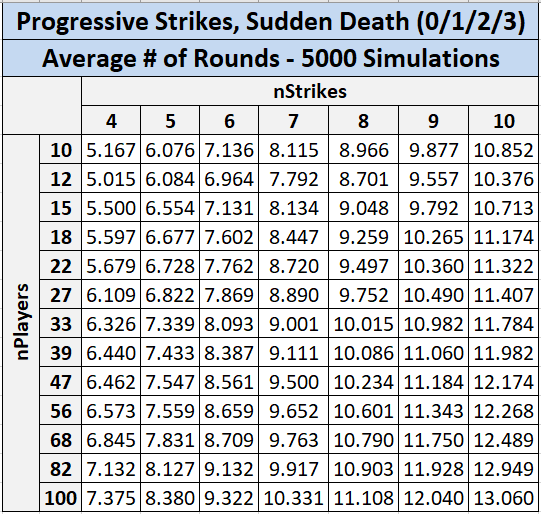
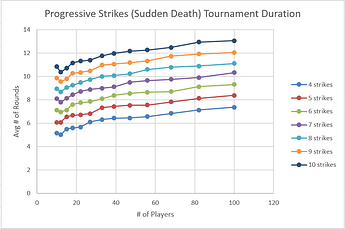
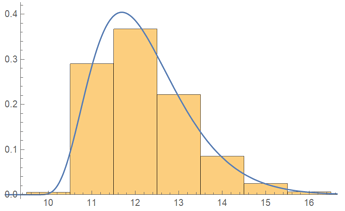
In case anyone’s interested in seeing the Mathematica code I used, here it is (including the narrower game score distribution to better separate skill levels, as well as sudden death for progressive strikes).
(* create a new player with a random skill level, 0 strikes/games *)
(* {playerID, skill, {round opponents}, strikes} *)
MakePlayer[ID_] := {ID, RandomVariate[LogNormalDistribution[0, 0.25]], {}, 0}
(* create a list of n new players *)
MakePlayers[n_] := MakePlayer[#] & /@ Range[n]
(* game score for a single player *)
GameScore[skill_] := RandomVariate[LogNormalDistribution[skill, 0.25]]
(* game scores for all players *)
GameScores[players_] := GameScore[#[[2]]] & /@ players
(* rank players by game score *)
GameRanking[players_] := Module[{scores, sortedScores, ranks},
scores = GameScores[players];
sortedScores = Reverse@Sort@scores;
ranks = Flatten[FirstPosition[sortedScores, #] & /@ scores];
Return@ranks
]
(* run game for multiple players, update records & strikes *)
RunGame[players_, suddenDeath_] :=
Module[{playerIDs, skills, roundResults, strikes, ranks, updatedStrikes, newRoundResults, updatedRoundResults, updatedPlayers},
{playerIDs, skills, roundResults, strikes} = Transpose@players;
ranks = GameRanking[players];
newRoundResults = DeleteCases[playerIDs, #] & /@ playerIDs;(* list of opponents for each player *)
updatedRoundResults = MapThread[Append[#1, #2] &, {roundResults, newRoundResults}];
updatedStrikes = strikes + Switch[
1,
1, If[suddenDeath, 2 (ranks - 1), ranks - 1],(* 1 strike for each loss, doubled if sudden death *)
2, Switch[#, 1, 0, Length@players, 2, _, 1] & /@ ranks,(* fair strikes: 1st gets 0, last gets 2, else 1 *)
3, Sign[ranks - 1](* everyone except 1st gets a strike *)
];
updatedPlayers = Transpose@{playerIDs, skills, updatedRoundResults, updatedStrikes};
Return@updatedPlayers
]
(* partition players into groups of up to n, avoiding singletons *)
PartitionPlayers[players_, n_] := Module[{nPlayers, remainingPlayers, groups, finalPartition},
nPlayers = Length@players;
remainingPlayers = players;
groups = {};
If[nPlayers <= n,(* if players fit on one game *)
AppendTo[groups, remainingPlayers];
remainingPlayers = {};
];
While[Length@remainingPlayers > LCM[n, n - 1],(* while excess players exist *)
AppendTo[groups, Take[remainingPlayers, n]];(* take n of them *)
remainingPlayers = Drop[remainingPlayers, n]
];
finalPartition = First@SortBy[Select[IntegerPartitions[Length@remainingPlayers], Max@# <= 4 &], Length@# - Min@# &];(* partition final players to maximize minimum group size *)
Do[
AppendTo[groups, Take[remainingPlayers, finalPartition[[i]]]];(* take up to n of them *)
remainingPlayers = Drop[remainingPlayers, finalPartition[[i]]], {i, 1, Length@finalPartition}
];
Return@groups
]
(* run tournament round with nPerGame players per game *)
RunRound[players_, nPerGame_, suddenDeath_] :=
Module[{groups, updatedGroups},
groups = PartitionPlayers[players, nPerGame];
updatedGroups = RunGame[#, suddenDeath] & /@ groups;
Return@Flatten[updatedGroups, 1]
]
(* shuffle players and sort by strikes *)
SortByStrikes[players_] := SortBy[RandomSample[players], Last]
(* run tournament with nStrikes to be ejected *)
RunTournament[players_, nPerGame_, nStrikes_] :=
Module[{nRounds, remainingPlayers, removedPlayers, suddenDeath},
nRounds = 0;
remainingPlayers = players;
removedPlayers = {};
suddenDeath = False;(* flag set when 2 players remain *)
While[Length@remainingPlayers > 1,
nRounds++;
If[Length@remainingPlayers < 3, suddenDeath = True];(* 2 players left \[Rule] sudden death *)
remainingPlayers = RunRound[remainingPlayers, nPerGame, suddenDeath];
removedPlayers = Join[removedPlayers, Reverse@Select[remainingPlayers, Last@# >= nStrikes &]];
remainingPlayers = Select[remainingPlayers, Last@# < nStrikes &];
remainingPlayers = SortByStrikes[remainingPlayers]
];
Return@{nRounds, remainingPlayers, removedPlayers}
]
(* run Monte Carlo simulation of many tournaments to find duration (in rounds) *)
RunMonteCarloRounds[nPlayers_, nPerGame_, nStrikes_, nSims_] :=
Module[{results},
results = ParallelTable[First@RunTournament[MakePlayers[nPlayers], nPerGame, nStrikes], {i, 1, nSims}];
Return[results]
]
(* run tournament and calculate Kendall Tau coefficient of final rankings *)
TournamentKendall[nPlayers_, nPerGame_, nStrikes_] :=
Module[{nRounds, remainingPlayers, removedPlayers, IDs, skills, roundResults, strikes},
{nRounds, remainingPlayers, removedPlayers} = RunTournament[MakePlayers[nPlayers], nPerGame, nStrikes];
{IDs, skills, roundResults, strikes} = Transpose@Join[removedPlayers, remainingPlayers];
Return@KendallTau[Range[nPlayers], skills]
]
Once these functions are loaded, simulations can be run like this:
(* generate statistics on a specific tournament config *)
nPlayers = 33;
nPlayersPerGame = 4;
nStrikes = 10;
nSims = 5000;
data = RunMonteCarloRounds[nPlayers, nPlayersPerGame, nStrikes, nSims];
mean = N@Mean@data
stdev = N@Sqrt@Variance@data;
cov = stdev/mean;
SortBy[Tally[data], First] // TableForm // Print
hist = Histogram[data, Automatic, "ProbabilityDensity"];
dist = EstimatedDistribution[data, JohnsonDistribution["SB", \[Gamma], \[Delta], \[Mu], \[Sigma]]]
Show[hist, Plot[PDF[dist, x], {x, 0, 30}, PlotRange -> All]]