A topic I have been doing some research on is the idea of a round-robin, but a group match play round-robin as opposed to head-to-head to see there’s a way that you can play every opponent once and only once but still have games of either 3 or 4 players.
I came across this concept of a Social Square which seems to allow for just that (in specific cases):
https://www.devenezia.com/round-robin/forum/?topic=774
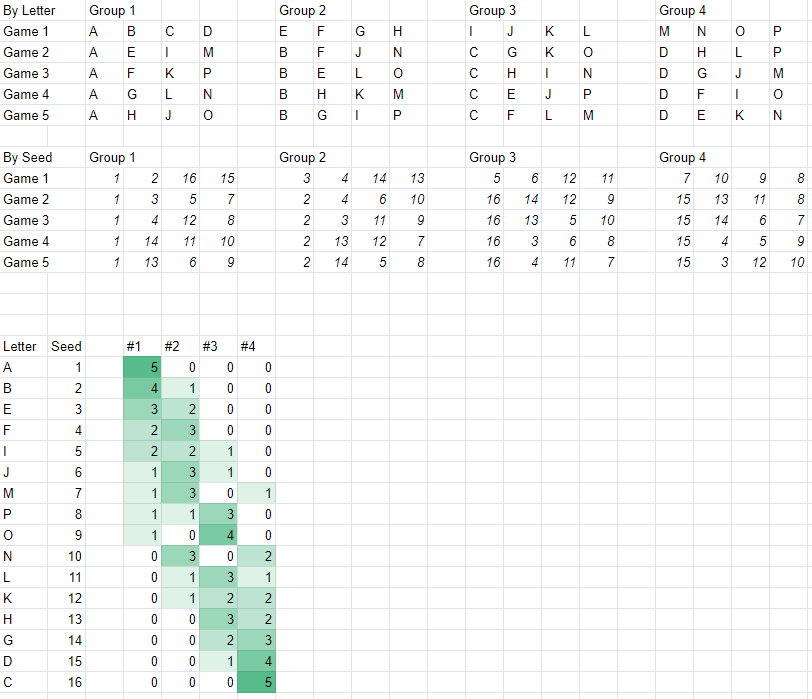
The example they cite is for 16 players:

If you are player A, then you need to face 15 unique opponents so you will need (15 / 3) = 5 Group Play matches to face everyone exactly once. Scoring is straight ahead. How many opponents did you win against?
I thought that this would be an interesting way to get what would essentially be head-to-head results over the course of five group-play matches as opposed to 15 rounds of Round-Robin.
I also thought that it would be an interesting way to conduct a Finals if you identity a Top 16. That being said, there’s a problem with the match-ups as laid out when it comes to seeding purposes. If you assume the order of the letters is the choice order, over the course of the matches it looks something like this:

You’re essentially locked into your position except when you’re playing in the match close to your “tier”.
I played with some of the letter/seed pairings to see if I could accomplish the following:
- Smooth the curve of the number of 1sts, 2nds, 3rds, and 4ths based on you seeding
- Avoiding playing everyone close to you in a single match (i.e. no match of 1-2-3-4, but spread those pairings out across those matches.
Here’s what I’ve come up with:
Long story short, I plan I conducting this type of Finals at an upcoming event that we’re running and will report back how it goes. My thought at the moment is that we’ll run qualifying, then these five rounds of Match Play and then do some kind of final round with the Top 4.
Beyond just 16 players, I think there’s an opportunity to make something like this work for a number of different player configurations, especially when there’s the opportunity to have either 4, 3, or 2-player matches.
For 9 players, you could do four 3-player matches and have everyone play everyone once. I haven’t optimized the seeds yet for this one to avoid a 1-2-3 matchup.
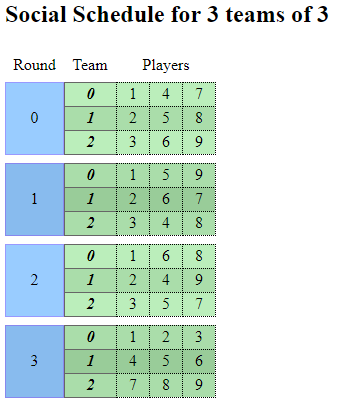
Source: https://www.devenezia.com/downloads/round-robin/social-square-prime.html
My spreadsheet: https://docs.google.com/spreadsheets/d/1b3n27p9KxDacZ6wc4-gP7f-JyX5zFHThFAgseFlmiCw/edit?usp=sharing
I’m interested to spend time over the next few weeks working out if configurations are possible from 9 players and up (can it work with 11? can it work with 24?) but wanted to put this out there for thoughts and feedback.