Motivation
This is a follow-up to the previous topic: https://tiltforums.com/t/strikes-tournament-simulation-results-part-2/9005
I write this to correct errors in the previous topic. ElDeco found a bug in my code, and then I found another similar bug.
The first bug was that the code which calculates Kendall Tau (a measure of how well the tournament sorts players by skill) was incorrectly placing the tournament winner in last place instead of first place. This has the effect of significantly depressing the Tau value, especially when the player count is low - hence the dubious shape of the Tau plots in the previous post.
The second bug was that the code which removes players who have exceeded the strikes threshold in each round was sorting them by their number of strikes, when it should have been reverse-sorting them. In other words, a player who exited the tournament with 11 strikes was being placed ‘ahead’ of a player who exited in the same round with only 10 strikes. This bug depressed the Tau value very slightly.
Player Model
I have updated the player model. Because of the bad code artificially depressing the Tau value, the game score scatter parameter was set too small. I have raised the game score scatter parameter to 0.57, which again brings the Tau value for 110-player 8 Fair Strikes tournaments to the target value of 0.45 (in keeping with the two District82 tournaments previously analyzed).
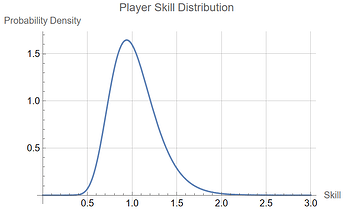
The player skill distribution still looks like this:
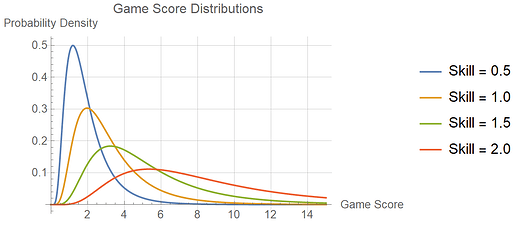
But now the game score distributions for players of skill 0.5, 1.0, 1.5, and 2.0 have a bit more overlap:
That means the chance for a lower-skill player to beat a higher-skill player is a bit higher than in my previous code. Here are the new probabilities:
- 0.5 vs. 1.0 skill: Higher skill player wins 73.2% of games
- 0.5 vs. 1.5 skill: Higher skill player wins 89.2% of games
- 0.5 vs. 2.0 skill: Higher skill player wins 96.9% of games
- 1.0 vs. 1.5 skill: Higher skill player wins 73.2% of games
- 1.0 vs. 2.0 skill: Higher skill player wins 89.2% of games
- 1.5 vs. 2.0 skill: Higher skill player wins 73.2% of games
Tournament Types
The following permutations were examined:
- Progressive Strikes, Fair Strikes, Lenient Group Strikes, Oprah Strikes, Single Strikes, and Head-to-Head Strikes (which puts 2 players on each game)
- A variety of strikes thresholds for exiting the tournament
- Attendance including every value from 10 to 150 players
Each permutation was given 5000 full simulations, and results were averaged to obtain the data points plotted below. Those results include:
- Average tournament length (in rounds)
- Average tournament duration (in a kind of pseudo-time)
- Average Kendall tau (a statistical measure of how well the tournament sorts players by intrinsic skill) - if the players were perfectly sorted, this would be 1.0, and if they were randomly sorted, this would be close to zero.
- TGP value, using the weighting of 1x for 2-player games, 1.5x for 3-player games, 2x for 4-player games
The definition of each tournament type is described here:
Progressive Strikes (Swiss Groupings)
4 players: 0/1/2/3 strikes
3 players: 0/1/2 strikes
2 players: 0/1 strikes
Fair Strikes (Swiss Groupings)
4 players: 0/1/1/2 strikes
3 players: 0/1/2 strikes
2 players: 0/2 strikes
Lenient Group Strikes (Swiss Groupings)
4 players: 0/0/1/1 strikes
3 players: 0/0/1 strikes
2 players: 0/1 strikes
Oprah Strikes (Swiss Groupings)
4 players: 0/1/1/1 strikes
3 players: 0/1/1 strikes
2 players: 0/1 strikes
Single Strikes (Swiss Groupings)
4 players: 0/0/0/1 strikes
3 players: 0/0/1 strikes
2 players: 0/1 strikes
Head-to-Head Strikes (Swiss Groupings)
2 players: 0/1 strikes
Results
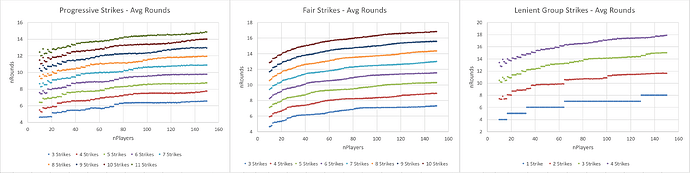
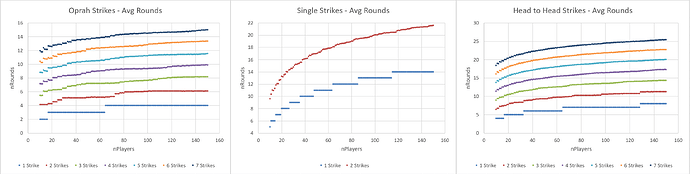
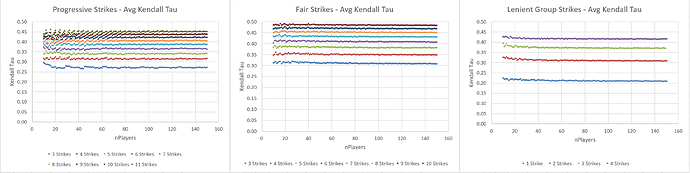
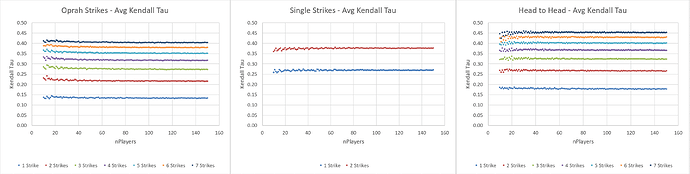
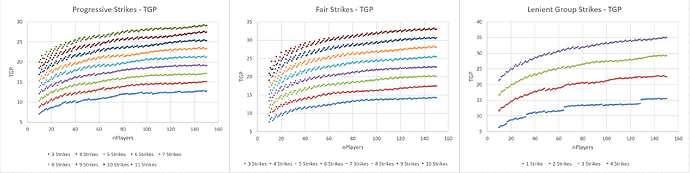
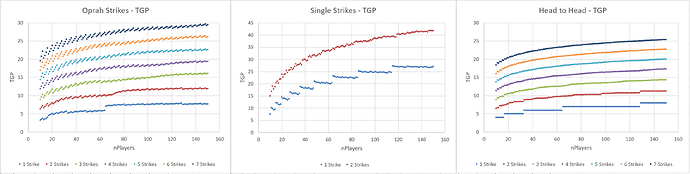
Average number of rounds for different tournament types and player counts:
Average Kendall Tau value:
TGP value (a weighted average proportional to number of rounds, and number of players per game in each round):
Results, Narrowed
Now to consider the more popular choices amongst tournament organizers:
- 10 Progressive Strikes
- 8 Fair Strikes
- 3 Lenient Group Strikes
- 7 Oprah Strikes
- 1 Single Strikes
- 6 Head-to-Head Strikes
7 Oprah Strikes may not be a popular format, but it’s comparable to the others in outcomes.
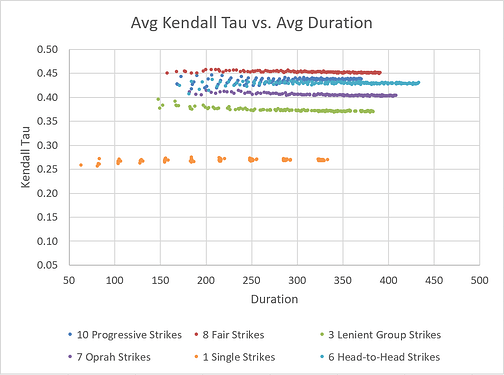
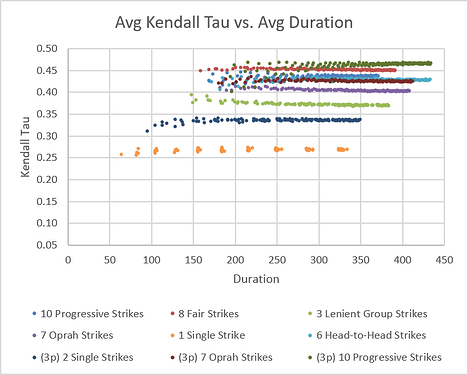
Comparing these formats by their ability to sort players by skill, we get this plot:
We can see that 1 Single Strikes (also known as ‘Don’t Be Last’) is the most chaotic format, while the others more strongly sort players by skill.
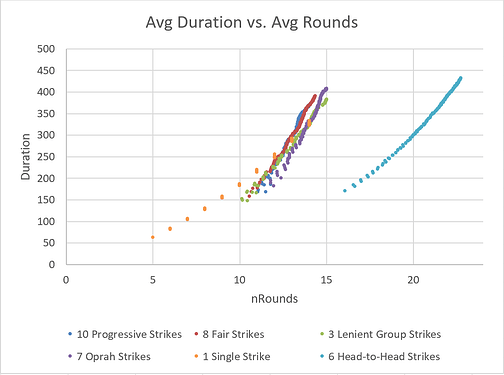
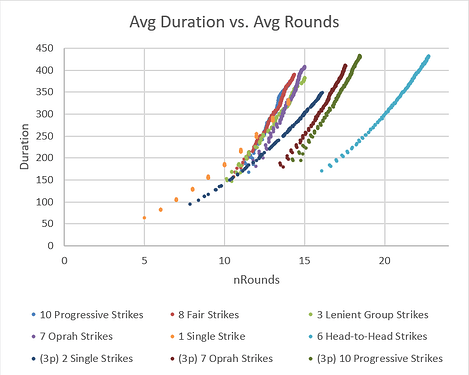
Next we plot average duration (in pseudo-time) against average number of rounds, to see if any format comes out ahead:
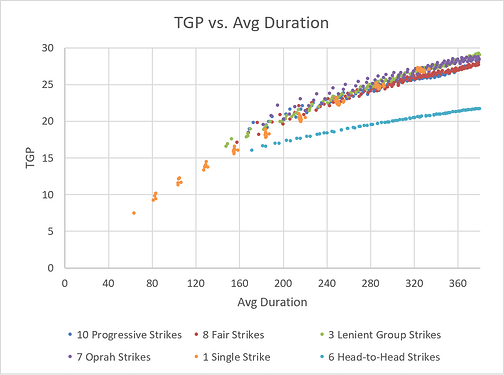
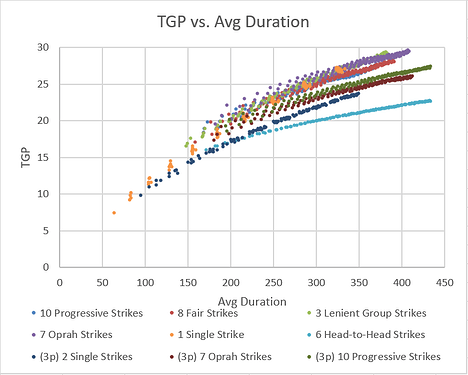
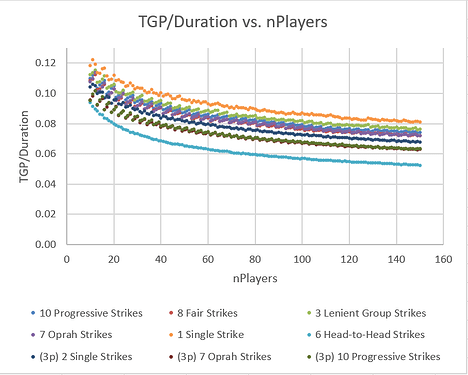
The major takeaway is that Head-to-Head tournaments have predictably shorter rounds. But how time-efficient are the different tournaments, given that players want to maximize their TGP?:
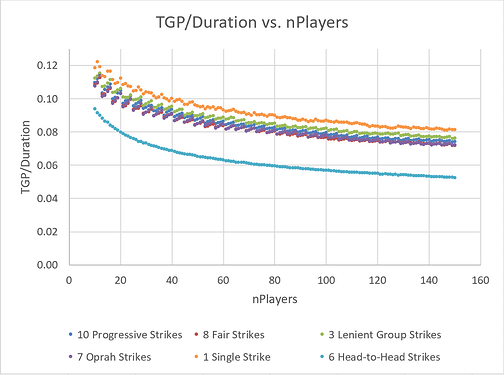
Here, Head-to-Head Strikes falls woefully short. My previous investigations determined this was due to the higher coefficient of variation in the duration of 2-player games, as compared to 4-player games. In a Head-to-Head tournament, each round is shorter, but more rounds are required, and the latter ends up dominating the former. The other tournament types with 4 players per game are all roughly comparable in efficiency.
Other Topics
My previous conclusion about Swiss groupings shortening tournaments’ runtime by 10% (relative to random groupings) remain unchanged.
Python Code, with bug fixes
import math
import numpy as np
from operator import add
from scipy import stats
import csv
# USER-DEFINED PARAMETERS
SIM_TYPE = "Monte Carlo" # "Monte Carlo" = average results for all permutations of N_PLAYERS and N_STRIKES
# "Histogram" = all results for N_PLAYERS_MIN and N_STRIKES_MIN
FORMAT = "Progressive Strikes" # Progressive Strikes [0,1,2,3]
# Fair Strikes [0,1,1,2]
# Oprah Strikes [0,1,1,1]
# Lenient Group Strikes [0,0,1,1]
# Single Strikes [0,0,0,1]
N_PER_GAME = 4 # nominal number of players on each game (player count permitting)
SWISS = True # True = Swiss groupings, False = random groupings
N_STRIKES_MIN = 3 # lowest strikes threshold for elimination (iterates from MIN to MAX)
N_STRIKES_MAX = 11 # highest strikes threshold for elimination
N_PLAYERS_MIN = 10 # lowest number of players in tournament (iterates from MIN to MAX)
N_PLAYERS_MAX = 150 # highest number of players in tournament
N_RUNS = 5000 # number of tournaments to simulate for each format and player count (higher = better statistics)
SKILL_SCATTER = 0.25 # second parameter of lognormal distribution of player skill
SCORE_SCATTER = 0.57 # second parameter of lognormal distribution of game score
RAND_SEED = 42 # starting seed for random number generator
# a player in a strikes-based tournament
class Player(object):
def __init__(self, ID):
self.ID = ID
self.skill = rand.lognormal(0, SKILL_SCATTER)
self.games = []
self.strikes = 0
self.bounties = 0
# generate a game score
def gameScore(self):
return rand.lognormal(self.skill, SCORE_SCATTER)
# store a game in memory
def recordGame(self, game):
self.games.append(game)
# receive strikes & add to total
def addStrikes(self, strikesGiven):
self.strikes += strikesGiven
# capture bounties & add to total
def addBounties(self, bountiesCaptured):
self.bounties += bountiesCaptured
# a strikes-based tournament
class Tournament(object):
def __init__(self, nPlayers, nPerGame, format, nStrikes):
self.nPlayers = nPlayers
self.nPerGame = nPerGame
self.format = format
self.nStrikes = nStrikes
self.players = []
self.eliminatedPlayers = []
self.groups = []
self.numInRound = []
self.roundDuration = 0
self.totalDuration = 0
self.nRounds = 0
self.suddenDeath = False
self.tau = 0
self.tgpGameCounts = [0 for i in range(nPerGame - 1)] # counts of m-player games played in tournament, where m = 2 to nPerGame
# initialize list of players
def initPlayers(self, n):
self.players = [Player(i) for i in range(n)]
# shuffle player order
def shufflePlayers(self):
rand.shuffle(self.players)
# sort remaining players by strikes (stable sort)
def sortByStrikes(self):
self.players.sort(key=lambda p : p.strikes)
# partition players into groups of at most n
def partitionPlayers(self, n):
if len(self.players) <= n: # if all players fit in one group
self.groups.append(self.players)
self.players = []
while len(self.players) > math.lcm(n, n-1): # while many players remain, group them n at a time
self.groups.append(self.players[:n])
self.players = self.players[n:]
potentialPartitions = [i for i in [*partitions(len(self.players))] if max(i) <= n]
potentialPartitions.sort(key = lambda x : min(x))
chosenPartition = potentialPartitions[-1] # choose partition with largest minimum group size
for i in sorted(chosenPartition, reverse=True):
self.groups.append(self.players[:i])
self.players = self.players[i:]
for g in self.groups:
if len(g) > 1:
self.tgpGameCounts[len(g) - 2] += 1 # add number of 2-, 3-, 4-player game counts to tournament totals
# each group plays their game
def runGames(self):
self.roundDuration = 0
for g in self.groups:
IDs = [p.ID for p in g]
scores = [p.gameScore() for p in g]
self.roundDuration = max(self.roundDuration, sum(scores)) # round duration is equal to the largest sum of players' scores on a game
sortedScores = sorted(scores, reverse=True)
ranks = [positions(sortedScores, lambda x : x == s)[0] for s in scores]
strikesGiven = strikesGen(self.format, ranks) # determine strikes given to each player
for i in range(len(g)):
g[i].addStrikes(strikesGiven[i]) # assign strikes
for p in g:
p.games.append(IDs) # record player IDs
nElim = len([1 for p in g if p.strikes >= self.nStrikes]) # number of players in group who are eliminated
iWin = positions(ranks, lambda x : x == 0) # indices of group winners
if nElim > 0:
g[iWin[0]].addBounties(nElim) # winner collects all bounties
# remove eliminated players & return other players to main pool
def cleanup(self):
self.players = [p for g in self.groups for p in g if p.strikes < self.nStrikes]
self.eliminatedPlayers.append(sorted([p for g in self.groups for p in g if p.strikes >= self.nStrikes], key = lambda p : p.strikes, reverse=True))
self.groups = []
# run rounds until one person remains
def runTourney(self):
self.initPlayers(self.nPlayers)
while len(self.players) > 1:
self.nRounds += 1
self.numInRound.append(len(self.players))
self.shufflePlayers() # randomize player order
if SWISS:
self.sortByStrikes()
self.partitionPlayers(self.nPerGame)
# print("ROUND", self.nRounds, ":", len(self.players), "remaining. Top group:", [p.strikes for p in self.groups[0]])
self.runGames()
self.cleanup()
self.totalDuration += self.roundDuration
self.kendallTau()
# compute Kendall's tau, a measure of how well the tournament ranked the players by intrinsic skill
def kendallTau(self):
rankedPlayers = [p for round in self.eliminatedPlayers for p in round]
rankedPlayers.insert(-1, self.players[0])
ranks = range(len(rankedPlayers))
skills = [p.skill for p in rankedPlayers]
tau, p_value = stats.kendalltau(ranks, skills)
self.tau = tau
# report tournament results
def report(self):
print("After", self.nRounds, "rounds")
print("The winner is: Player", self.players[0].ID, "with", self.players[0].strikes, "strikes")
print("Winner's games played:")
for g in self.players[0].games:
print(g)
# return positions of list items matching a predicate
def positions(list, predicate):
return [i for i, v in enumerate(list) if predicate(v)]
# signum function
def sign(x):
if x > 0:
return 1
elif x < 0:
return -1
else:
return 0
# generator for integer partitions
def partitions(n, I=1):
yield (n,)
for i in range(I, n//2 + 1):
for p in partitions(n-i, i):
yield (i,) + p
# determine strikes assigned to each rank for a game result
def strikesGen(format, ranks):
n = len(ranks)
strikes = []
if format == "Progressive Strikes":
return ranks # strikes equal ranks; [0, 1, 2, 3]
elif format == "Fair Strikes":
for i in range(n):
strikes.append(sign(ranks[i]) + (1 - sign(n - 1 - ranks[i]))) # strikes = [0, 1, 1, 2]
elif format == "Oprah Strikes":
for i in range(n):
strikes.append(sign(ranks[i])) # all but winner get a strike; [0, 1, 1, 1]
elif format == "Lenient Group Strikes":
s = math.ceil(n/2)
for i in range(n):
if ranks[i] >= s:
strikes.append(1) # worse half of players get a strike, lenient when n=odd [0, 0, 1, 1]
else:
strikes.append(0)
elif format == "Single Strikes":
for i in range(n):
strikes.append(math.floor(ranks[i]/(n - 1))) # lowest score gets a strike; [0, 0, 0, 1]
else:
for i in range(n):
strikes.append(1) # give everyone a strike
return strikes
# return stats on tourney
def tourneyStats(nPlayers, nPerGame, format, nStrikes, nRuns):
roundsData = []
durationData = []
tauData = []
bountyData = []
tgpGameCounts = [0 for i in range(nPerGame - 1)]
for i in range(nRuns):
tourney = Tournament(nPlayers, nPerGame, format, nStrikes)
tourney.runTourney()
roundsData.append(tourney.nRounds)
durationData.append(tourney.totalDuration)
tauData.append(tourney.tau)
bountyData.append(tourney.players[0].bounties)
tgpGameCounts = list(map(add, tgpGameCounts, tourney.tgpGameCounts))
avgRounds = np.mean(roundsData)
avgDuration = np.mean(durationData)
avgTau = np.mean(tauData) # average Kendall tau of rankings
avgBounties = np.mean(bountyData) # average bounties collected by winning player
tgpMultipliers = [0.5*i + 1 for i in range(nPerGame - 1)] # TGP multipliers for 2-, 3-, 4-player games, etc.
tgpNetMultiplier = sum([x*y for x, y in zip(tgpGameCounts, tgpMultipliers)]) / sum(tgpGameCounts) # overall multiplier for tournament config
tgpFinal = avgRounds*tgpNetMultiplier
return (avgRounds, avgDuration, avgTau, avgBounties, tgpFinal)
# return histogram on tourney
def tourneyHist(nPlayers, nPerGame, format, nStrikes, nRuns):
roundsData = []
durationData = []
tauData = []
bountyData = []
for i in range(nRuns):
tourney = Tournament(nPlayers, nPerGame, format, nStrikes)
tourney.runTourney()
roundsData.append(tourney.nRounds)
durationData.append(tourney.totalDuration)
tauData.append(tourney.tau)
bountyData.append(tourney.players[0].bounties)
return (roundsData, durationData, tauData, bountyData)
### -------- SCRIPT -------- ###
# initialize random generator
rand = np.random.RandomState(RAND_SEED)
# Monte Carlo statistics for many tournament configurations
if SIM_TYPE == "Monte Carlo":
nStrikes = range(N_STRIKES_MIN, N_STRIKES_MAX + 1)
nPlayers = range(N_PLAYERS_MIN, N_PLAYERS_MAX + 1)
iMax = len(nStrikes)
jMax = len(nPlayers)
for i in range(iMax):
print("starting on", nStrikes[i], "strikes")
fileID = str(nStrikes[i]).zfill(2)
filename = FORMAT + " " + fileID + ".txt"
f = open(filename, 'w')
writer = csv.writer(f)
for j in range(jMax):
print(nPlayers[j], "players")
avgRounds, avgDuration, avgTau, avgBounties, tgpValue = tourneyStats(nPlayers[j], N_PER_GAME, FORMAT, nStrikes[i], N_RUNS)
writer.writerow([avgRounds, avgDuration, avgTau, avgBounties, tgpValue])
f.close()
# complete data for a single tournament configuration (useful for making histograms)
if SIM_TYPE == "Histogram":
roundsData, durationData, tauData, bountyData = tourneyHist(N_PLAYERS_MIN, N_PER_GAME, FORMAT, N_STRIKES_MIN, N_RUNS)
filename = FORMAT + " " + str(N_STRIKES_MIN).zfill(2) + " " + str(N_PLAYERS_MIN).zfill(2) + " histogram.txt"
f = open(filename, 'w')
writer = csv.writer(f)
for i in range(len(roundsData)):
writer.writerow([roundsData[i], durationData[i], tauData[i], bountyData[i]])
f.close()
Thanks again to ElDeco for spotting the bug!