I haven’t read every post in this thread, but I understand there are questions about how well different qualifying rules end up sorting players by skill.
I have some existing code which may help to answer these questions. It assumes players have an intrinsic skill, which is of course an oversimplification.
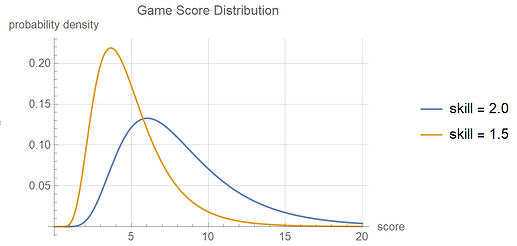
I’m using the same lognormal distributions I’ve used previously for player skill and game score (see post history). Specifically, player skill is distributed according to lognormal(0, 0.25), and a player’s score on a game is distributed according to lognormal(skill, 0.45). In other words, the scatter parameter on player skill is 0.25, and the scatter parameter on game score is 0.45, with players of higher skill getting higher scores on average. But there is always a chance a lower-skill player wins.
Note about Kendall Tau parameter:
The Kendall Tau parameter measures how well the elements of two vectors match each others’ sorting order. If the vectors are perfectly sorted - that is, if qualifying perfectly sorts players by their intrinsic skill - the Tau parameter equals 1. If the rankings are completely uncorrelated to skill, the Tau parameter will be ~0. And if it sorts them exactly backwards by skill, the Tau parameter will be -1.
Experiment 1:
100 players attempt to qualify, each with randomly determined intrinsic skill. Each players plays one game nPlays times, keeping their best score. After the results are collected, the Kendall Tau parameter is used to evaluate how well the qualifying sorted the players according to their intrinsic skill parameter. This simulated qualifying is repeated 5000 times, to obtain an accurate average for Tau.
| nPlays |
Avg Kendall Tau |
| 1 |
0.327 |
| 2 |
0.381 |
| 3 |
0.412 |
| 4 |
0.432 |
| 6 |
0.458 |
| 8 |
0.476 |
| 12 |
0.500 |
| 16 |
0.514 |
| 24 |
0.534 |
We can see a larger number of plays on a game better sorts players by intrinsic skill. However, Tau grows relatively slowly with respect to nPlays, and therefore slowly with respect to the duration of qualifying.
Additionally, it is not clear that a higher value of Tau is better than a lower one. If Tau is 0, the tournament has no sorting power and chaos reigns. But if Tau is 1, the tournament can have no surprises. Presumably, a value in-between 0 and 1 is preferred.
Experiment 2:
Let us consider the number of plays a weaker player would need to have a ~50% chance of out-qualifying a stronger player on a particular game. The stronger player plays the game nA times, while the weaker player plays it nB times. Various combinations of nA and nB are tried to determine how much more effort the weaker player must exert to match the results of the stronger player. The simulation is run 1 million times for each configuration to obtain a good probability estimate.
Stronger player skill = 2.0, representing a top-tier player
Weaker player skill = 1.5, representing a strong player, but a noticeable step down in skill
| nA |
nB |
Player B win chance (%) |
| 1 |
1 |
21.6 |
| 2 |
2 |
17.0 |
| 3 |
3 |
14.6 |
| 4 |
4 |
12.9 |
| 5 |
5 |
11.9 |
| 1 |
2 |
33.5 |
| 1 |
3 |
41.3 |
| 1 |
4 |
47.0 |
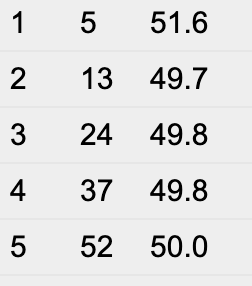
| 1 |
5 |
51.6 |
| 2 |
13 |
49.7 |
| 3 |
24 |
49.8 |
| 4 |
37 |
49.8 |
| 5 |
52 |
50.0 |
If both players play an equal number of games, the weaker player B’s chances dwindle as the number of games increases. A 21.6% chance of out-qualifying player A when they play 1 game each shrinks to a 11.9% chance when they play 5 games each.
We can see that the amount of work the weaker player B must do to have a 50% chance of out-qualifying the stronger player A increases as player A plays more games. The increase is faster than linear, as a result of the exponential tails of the distributions.
If player A plays 1 game, player B needs an average of ~5 games (about 5 times as many attempts) to reach parity.
However, if player A plays 5 games, player B needs an average of 52 games (more than 10 times as many attempts) to reach parity.
Conclusions:
Surprising absolutely no one, the longer qualifying lasts, the better it is at sorting players by intrinsic skill. The longer qualifying lasts, the lower the probability that weaker players will get lucky and out-qualify stronger players.