If there is little real difference between 0 and 25 I’m not in favor of showing 25 just because it appears to mean something to the uninitiated. There are better ways to counter the demoralizing effect of a poor performance.
Like giving them money for not winning!!!
I think it’s time to go Herb OG and bring back the 10 point scale . . .
LOL! And 2nd back in those days as well Josh! 
Sanjay, you beat me to it!
We used a similar system back in the … wait for it … 1970’s, except we gave points to the top 12 scores on each machine: 15, 12, 10, 9, 8, etc. Took either 8, 16, or in one case 10 for playoffs.
I’ve played in tournaments where top score gets 100 points (or whatever), and all the other scores get whatever percentage they are of the top score. So, basically just PAPA’s insane “total points scored on a ticket” method, which @Adam mentioned, except it normalizes scores between machines.
This seems fair to me, it mitigates the scaling issues, and the bonus for top scores depends on how much better those scores actually were. Are there any disadvantages I’m not seeing? I suspect one reason this isn’t widely used is that historically it has been hard to do.
At first glance that seems like a poor system because games can have such different scoring curves. A game that scores exponentially like BSD is very different from a game with more linear scoring like Grand Prix. Under that system the results for those games would reward players very differently for similar performances.
On top of that, the live results would be super volatile. You may have a comfortable qualifying ticket, then someone drops a huge bomb on a game or two where you were sitting well, then all of a sudden you have 70 points instead of 90 (or whatever) on those games.
I can see how different scoring curves might be an issue, but I think @timballs mentioned in the other thread that actual qualifying scores usually wind up in a lognormal distribution regardless of the game. Is PAPA qualifying data publicly available somehwere? I’d like to see how this would work out on real data.
As for the volatility, I suppose that comes down to preference. If someone manages to drop a huge bomb, my feeling is that this sets a new standard as to what’s possible to do on that machine, so it’s fair to devalue the other scores based on the margin by which they failed to hit that target. I get that that’s a different qualifying paradigm than the fixed scale ones in this thread.
The problem with this is if the top score is way better than the second best score, then all the other scores are bunched together near the bottom and the game is almost meaningless for everyone except the top player. For example if the top score was 10 times better than the second best score, then 1st gets 100, 2nd gets 10, and last place gets at worst 0 which is only 10 points less than 2nd place. If the scores were all the same except the top score was only twice the second best score, then 2nd gets 50 and last place may be 50 points worse than 2nd place.
Now if someone really wants to compare the relative strength of scores on a game I would suggest the following method, although this method would probably be too confusing to use as a scoring system in a qualifying event.
Take the logarithm of all the scores [call that log(score)], then find the average and standard deviation of those numbers, then assign a value for each log(score) based on how many standard deviations each is above or below the average.
This reasoning behind this is that the scores on a game generally appear to be a log-normal distribution. Taking the log of these scores will give a normal distribution. A log-normal distribution will have small gaps between the lower scores but as you go up to the higher scores the gap between successive scores gets bigger and bigger, which is typically what you see on pinball games.
What this would mean practically speaking is that the ratio of any two scores determines how much better one is. For example, how much better a score of 8M is compared to 4M is the same as how much better 4M is compared to 2M.
Overall this scheme would do a better job of taking into account how close or spread out the scores were. If the top score were 5M, but scores were evenly spread out up to 5M then the 5M wouldn’t be worth as much as if all the other scores were less than 2M.
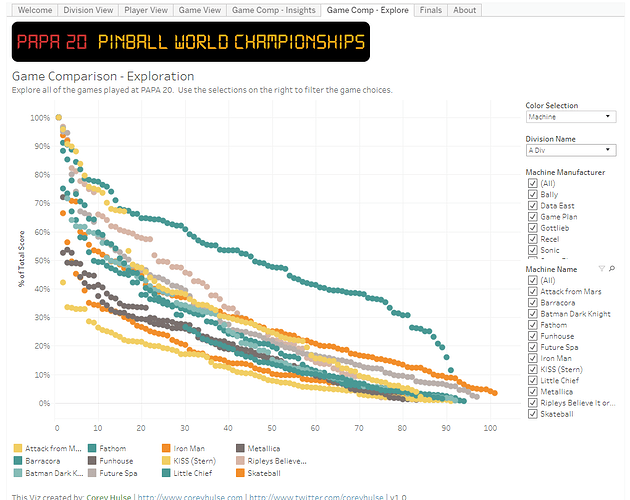
I made a Tableau Public app a while ago for PAPA 20: https://public.tableau.com/profile/corey.hulse#!/vizhome/PinballWorldChampionships/Welcome
Data here: PAPA20ScoresExtract.xlsx - Google Sheets
You can click on the game scores and see a scale for each.
A-Division at a glance:
Works best on the desktop; doesn’t work very well on mobile.
All the Match Play data is public. Not as popular a choice for large Best Game tournaments but there are some sizable classics tournaments in the database
It gets really weird late in qualifications for most formats. people can Feel like they are “in” with scores on say AFM and #1 at 10B. Then, last minute, someone drops a monster 100B game and the points anyone except #1 is getting from that game is essentially 0.
Scoring inception: you get points based on a percentage of the median score
Additionally if someone drops a bomb on a game, fewer players will want to play it, since decent scores are now worth pity points.
I have a bad cold right now so my head’s all fucked up, but what if you limited how “badly” an outlier could be to something like 20-25%? Here’s an example:
- AFM score 1 is currently 10B.
- Someone puts up the fabled 100B all of a sudden.
- Because of (say) the 25% cap, the actual score is effectively 12.5B.
- Old player 1 with his 10B now has 80 points, and everyone else goes down as a result of the 12.5B “top score”.
- Player 3 comes along and puts up a 16B. Player 2’s score now automatically becomes 20B (because he really scored 100B), Player 3 gets the 80 points, and Player 2 is down to 50.
Yes it still has the problem that a few outliers can still squash everyone else’s hopes and dreams, but the damage at least is mitigated for a singleton. You can pick whatever percentage is deemed least damaging, too.
I’d be lying, though, if I claimed I didn’t chuckle at the thought of one person crashing dozens of people’s standings, heh.
Even better(?), standard deviations?
I ran a comp a few years ago trying a different ranking system. I don’t have the details to hand right now, but will search them out, maybe @Robotgreg can find the email trail.
Each score on a machine was ranked with the average score getting 50, top score getting 100, and bottom score getting 1. Scores in between were scaled linearly between these 3 fixed points. (A simple formula in the excel sheet took care of all of this).
Each player only played each game in the lineup once, so there was no veering away from machines with massive scores.
On the day 1 person scored a massive score on 1 machine, 6-7 times the 2nd place score. There were no other massive outliers.
I compared the results with this scoring system, as opposed to the standards (100,95,90 - 100,90,85 & 100,99,98). The ONLY difference in the personnel qualifying was the person who put up the massive score qualified in 2nd as opposed to just missing out on the bubble of 5th. Personally I feel that such a great game deserves an extraordinary reward.
It’s the only time that I ever ran that scoring system, partly because the venue shut, but mainly that people found it a little confusing (but that may well have been because it was the first time it was used, and/or my explanation of said ranking system) - it certainly wasn’t because it through up crazy results.