I thought you’d all be interested a little pet project I’ve been working on. I am generally interested in learning more about data mining/machine learning techniques, and naturally decided the funnest way to learn more would be to use pinball data. I’m also super excited about Pinburgh, and figured that would be a good place to start. The advantage of Pinburgh is that it’s a pretty good sized data set.
Disclaimer I am not a machine learning expert. My training is with standard statistical models (i.e., Regression, ANOVA, etc.). So take the results with a grain of salt. If you think I did something wrong, please comment below and I’ll try to update.
Dataset
I constructed a data set that used Pinburgh 2015 division qualifications, Glicko rating at time of tournament, and WPPR ranking at the time of tournament.
One issue with predicting Divisions using WPPRs is that Pinburgh has division restrictions that prevent players from playing in certain divisions. One of those restrictions is WPPR rank. For this reason, I used the earned division qualification of the player instead of the actual division they played in ( E.g., if a player got 34 wins, they were placed in A division. If a player who was restricted to A got 31 wins, they counted as having qualified in B, even though they actually played in A). This only happened a handful of time.
Methods
I used the ‘partykit’ package in R to construct a conditional inference tree model to predict the earned division of each player. A bit about conditional inference trees from the authors of ‘partykit’…
“Conditional inference trees estimate a regression relationship by binary recursive partitioning in a conditional inference framework. Roughly, the algorithm works as follows: 1) Test the global null hypothesis of independence between any of the input variables and the response (which may be multivariate as well). Stop if this hypothesis cannot be rejected. Otherwise select the input variable with strongest association to the response. This association is measured by a p-value corresponding to a test for the partial null hypothesis of a single input variable and the response. 2) Implement a binary split in the selected input variable. 3) Recursively repeate steps 1) and 2).” (see partykit for more info)
##Results
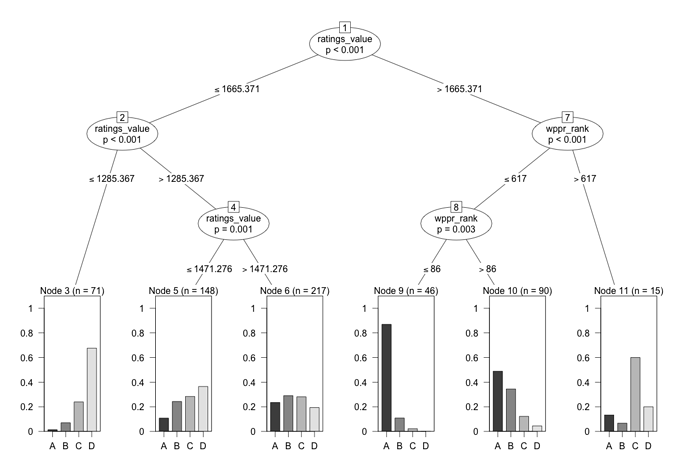
I ran several different models, but in the interest of not making the worlds longest post, I’ll only post one. This model tries to predict the expected division of a player based on their Glicko rating and WPPR rank at the time of the tournament. The final tree is shown below.
The tree is fairly simple to interpret. Follow each node like a flowchart, starting at the top node and working your way down. The terminal nodes at the bottom break down the probabilities of being in each division for each node. So you can basically use this tree to estimate the likelihood that a player of given rating and wppr rank will qualify in the A,B,C, or D division.
The most interesting finding here is the split on Node 8. Here, there is a pretty good distinction between players ranked better than 86 and players ranked worse than 86. If you are 86 or better (and have a rating greater than 1665), your chances of earning a seat in the A division are about 85%. If your rank is worse than 86, that likelihood drops to around 50. The split at node 7 was also rather interesting. The algorithm decided that a rank of 617 was a meaningful split. As can be seen on Node 11, the players rated higher than 1665 but ranked worse than 617 had a much lower probability of getting into A or B, and an elevated chance of being placed in C. There was only 15 players in this node, so I’m not sure how meaningful it actually is.
What is the accuracy of this model? If we run the model on the full dataset, and predict a player will be placed in a division with the greatest probability of their node, it yields an error rate of about 56%. Which is not super great (chance would be 75% error). But remember, were trying to predict 1 of 4 divisions. If we were just limiting the prediction to “A” or “Not A”, the error rate would be much better. It’s also worth mentioning that the error rate changes depending on Node, which affects the overall error rate. Certain nodes are more error prone than others. The full breakdown of node error rate is below.
Model formula:
earned_div ~ wppr_rank + ratings_value
Fitted party:
[1] root
| [2] ratings_value <= 1665.371
| | [3] ratings_value <= 1285.367: D (n = 71, err = 32.4%)
| | [4] ratings_value > 1285.367
| | | [5] ratings_value <= 1471.276: D (n = 148, err = 63.5%)
| | | [6] ratings_value > 1471.276: B (n = 217, err = 71.0%)
| [7] ratings_value > 1665.371
| | [8] wppr_rank <= 617
| | | [9] wppr_rank <= 86: A (n = 46, err = 13.0%)
| | | [10] wppr_rank > 86: A (n = 90, err = 51.1%)
| | [11] wppr_rank > 617: C (n = 15, err = 40.0%)
There are several nodes that don’t present a clear winner (e.g., nodes D and B), and their error percentages are (not surprisingly) very high. These error rates are closing in on the ballpark of chance. But of course, the probability breakdowns in those nodes show that each division is about equally probable. The ratings and wppr ranks just don’t provide much in the way of predictive power at that end of the scale.
Final Remarks
This was a pretty fun project, and the results were interesting. On a personal note, I remember being bummed that I didn’t qualify for A Division in 2015. It was somewhat comforting to find out that my rating and wppr ranking put me at about a 50% chance of getting into the A division. It made me feel a little less bad about it!
I welcome any comments and suggestions for alternate methods. If I committed an error, please call me out on it. A conditional inference tree is only one way of doing this kind of analysis, and I’m sure there are better ways. It will be interesting to see how well this model holds up for the 2016 results. Once the final player list is posted, I’ll try and follow up with predictions for everyone’s division.